√画像をダウンロード serie taylor log(1 x) 550482-Serie di taylor log(1+x)

What do you get when you plug a in?If you know Lagrange's form of the remainder you should not need to ask Also you haven't said what point you are expanding the function about (although it must be greater than ) The first derivative of is , The th derivative isHi!Learn to find the series expansion of log(1x) and log(1x) here

Solved The Maclaurin Series Expansion For The Natural Log Chegg Com

Serie di taylor log(1+x)

Serie di taylor log(1+x)-Sep 18, 11 · In taylor series if f(x)=log(1x) then is f'(a)=0?(x x 0)n (closed form) The Maclaurin series for y = f(x) is just the Taylor series for y = f(x) at x 0 = 0 1Here we are assuming that the derivatives y = f(n)(x) exist for each x in the interval I and for each n 2N f1;2;3;4;5;

Finding Radius And Interval Of Convergence Of A Taylor Series Krista King Math Online Math Tutor

Taylor expansion of 1 x The Taylor series for f Table 1 Taylor Series for f ⁢ (x) = 1 x The general coefficient of the expansion, for nPar exemple 4, si f(x) = exp(–1/x 2), prolongée par continuité en 0 par f(0) = 0, alors f est indéfiniment dérivable en tout point, et toutes les dérivées de f sont nulles en x = 0, donc la somme de la série de Taylor de f est nulle (et son rayon de convergence est infini), alors que la fonction n'est jamais nulle, sauf en 0Get the free "Log(1x) Taylor Series" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Mathematics widgets in WolframAlpha

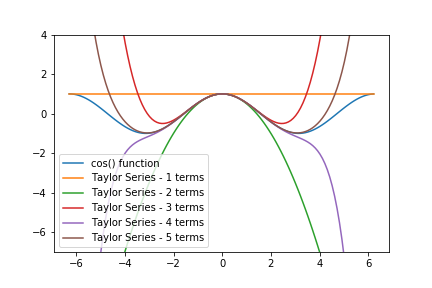
What is the general expression for the nth term in the Taylor series at x = 0 for In (1 4x5) ?Dec 21,  · In fact, the Taylor polynomials centered at 0 for 1 1−x converge to 1 1−x on the interval (−1, 1) and diverge for all other values of x So the Taylor series for a function \(f (x)\) does not need to converge for all values of \(x\) in the domain of \(f\)Oct 09, 19 · A Taylor series provides us a polynomial approximation of a function centered around point a Because the behavior of polynomials can be easier to understand than functions such as sin(x), we can use a Taylor series to help in solving differential equations, infinite sums, and advanced physics problems

This series was first described by Isaac Newton Remember the formula for the geometric series 1 − 1 x = 1 x x 2 x 3 ··· if x < 1 If we replace x by −x we get 1 1 x = 1 − x x 2 − x 3 ··· R = 1 You may recall that the graph of this function has an infiniteTruncation order of Taylor series expansion, specified as a positive integer or a symbolic positive integer taylor computes the Taylor series approximation with the order n 1 The truncation order n is the exponent in the Oterm O(var n)1−x PRELIMINARIES The function f(x) = log 1 1−x has a Taylor series representation centered about x 0 = 0 log 1 1−x = X∞ k=1 xk k, −1 ≤ x < 1 The nth Taylor polynomial of f(x) is given by T n(x) = k=1 xk k = x 1 2 x··· 1 n xn For a fixed x, the nth remainder term can be written as R n(x) = (1−c)−(n1) (n1) xn1

03 Truncation Errors

Taylor Series Wikipedia

Jan 29, 16 · How can you find the taylor expansion of #ln(1x)# about x=0?Jan 31, 18 · Let's say we wanted a Taylor series approximation for ln(1 x) about a = 2 Then, the series will converge for the values of x within the interval of convergence The lefthand point is 1Dec 29, 14 · Logarithms of Taylor Expansions I've already described how Herbie computes series expansions to produce polynomial approximations to floatingpoint programs There, I described how expansions of exponentials and the trigonometric functions worked, but I didn't have a way to expand logarithms and thus powers

Pdf A New Hardware Implementation Of Base 2 Logarithm For Fpga

Power Series Representation Of Ln 1 X Mathematics Stack Exchange

Find a series for f(x) = 2x / (1x 2) 2 Integration Start with a known series and integrate both sides Which function is represented by the series 1/n x n Multiplication Multiply two known series together until a pattern emerges Find the Taylor series centered at zero for f(x) = x 2 e 2xJan 02, 17 · The logic and context are not the same, as I was answering the question whether you can use the Taylor series In general, you prove the validity of the Taylor expansion over a given interval by proving the Taylor reminder tends to zero as n goes to infinityTopic Finding the Taylor Series of the Log(1x) or Log(1x) using the Geometric Series What you should know?

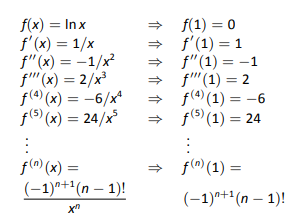
8 8 Taylor Series Mathematics Libretexts

Stpm Further Mathematics T 7 1 Taylor Polynomial

Let f(x)=log(1x) The Maclaurin expansion is f(x)=f(0) xf'(0) (x²/2!)f''(0) f(0)=log(10)=log(1)=0 f'(x)=Dlog(1x) f'(x)=1/(1x) f'(0)=1/(10)=1 f''(x)=1Jan 14, 18 · Convergent when xThere is no expansion around x = 1 because the log is highly singular at 1

Taylor Series For Ln 1 X How To Steps Math Class 21 Video Study Com

Cochranmath Taylor Series Integration And Differentiation

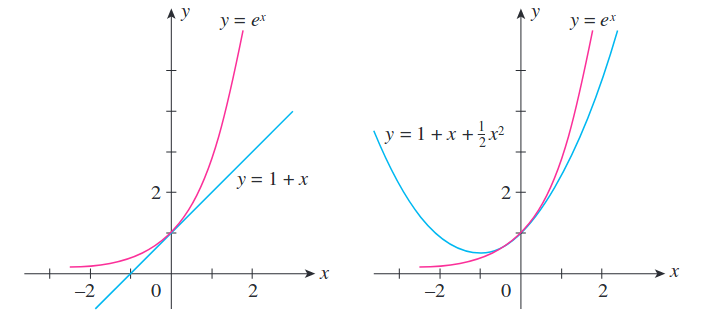
Dec 21,  · Earlier this semester, we saw how to approximate a function \(f (x, y)\) by a linear function, that is, by its tangent plane The tangent plane equation just happens to be the \(1^{\text{st}}\)degree Taylor Polynomial of \(f\) at \((x, y)\), as the tangent line equation was the \(1^{\text{st}}\)degree Taylor Polynomial of a function \(f(x)\)I need to nonlinearly expand on each pixel value from 1 dim pixel vector with taylor series expansion of specific nonlinear function (e^x or log(x) or log(1e^x)), but my current implementation is not right to me at least based on taylor series conceptsThe basic intuition behind is taking pixel array as input neurons for a CNN model where each pixel should be nonA Taylor Series is an expansion of some function into an infinite sum of terms, where each term has a larger exponent like x, x 2, x 3, etc Example The Taylor Series for e x e x = 1 x x 2 2!

Maclaurin Series For Ln 1 X Youtube

Power Series And Polynomial Approximation

Sep 03, 19 · Taylor series of log(x) with a = 1 Follow 103 views (last 30 days) Show older comments Ibrahima Diallo on 3 Sep 19 Vote 0 ⋮ Vote 0 Answered Kritika Bansal on 13 Sep 19 How to Write a Matlab function that sums up a specified number of terms from the Taylor series of log(x) with a = 1To get `tan(x)sec^3(x)`, use parentheses tan(x)sec^3(x) From the table below, you can notice that sech is not supported, but you can still enter it using the identity `sech(x)=1/cosh(x)` If you get an error, doublecheck your expression, add parentheses and multiplication signs where needed, and consult the table belowFree math lessons and math homework help from basic math to algebra, geometry and beyond Students, teachers, parents, and everyone can find solutions to their math problems instantly

Taylor Series Approximation Newton S Method And Optimization

Taylor Series For Ln 1 X How To Steps Math Class 21 Video Study Com

Calculus Power Series Constructing a Taylor Series 1 AnswerMay 26,  · In this section we will discuss how to find the Taylor/Maclaurin Series for a function This will work for a much wider variety of function than the method discussed in the previous section at the expense of some often unpleasant work We also derive some well known formulas for Taylor series of e^x , cos(x) and sin(x) around x=0Sep 03, 19 · Taylor series of log(x) with a = 1 Follow 54 views (last 30 days) Show older comments Ibrahima Diallo on 3 Sep 19 Vote 0 ⋮ Vote 0 Answered Kritika Bansal on 13 Sep 19 How to Write a Matlab function that sums up a specified number of terms from the Taylor series of log(x) with a = 1

Solved The Maclaurin Series Expansion For The Natural Log Chegg Com

Taylor Series Of Ln X Page 1 Line 17qq Com

O A 4x5 42x10 43x15 44x 2 3 4 4x10 4x15 OB 1 4x5 2 3 42x10 43x15 43x15 44x O C 4x5 2 3 4 4x10 4x ,15 3 4x OD 4x5Jan 14, 15 · Of course, this only refers to the vicinity of the point x_0=0 Often in Taylor series related homework tasks you'll face functions more complicated than just considered, also you can be asked to expand your function in the vicinity of different point than just zero Calculations thus are getting complicated and require your attention and timeFor b < 1, log b (x) tends to minus infinity instead When x approaches zero, log b x goes to minus infinity for b > 1 (plus infinity for b < 1, respectively) Derivative and antiderivative It is the Taylor series of the natural logarithm at z = 1 The Taylor series of ln(z)

I Am Taking A Taylor Series Expansion Of A Function F X I Wish To Expand The Function Around The Value G X Is This Allowable

What Is The Taylor Series Expansion Of 1 Log X About X 2 Quora

Σ n=1 What is the Taylor series for In (1 4x5) at x = 0?May 07, 19 · Expand log (1 sinx) up to the term containing x^4 by using Maclaurin's theorem asked May 7, 19 in Mathematics by AmreshRoy ( 695k points) differential calculusFunção seno de x e aproximações de Taylor com polinômios de grau 1, 3, 5, 7, 9, 11 e 13 9 A série de Taylor associada a uma função f {\displaystyle f} infinitamente diferenciável ( real ou complexa ) definida em um intervalo aberto a − r , a r é a série de potências dada por

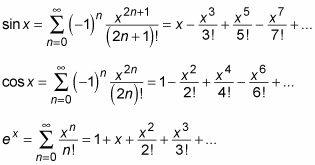
Determining Whether A Taylor Series Is Convergent Or Divergent Dummies

Introduction To Taylor S Theorem For Multivariable Functions Math Insight

What is the Lagrange remainder for a ln(1x) Taylor series?Feb 19,  · In this section we discuss how the formula for a convergent Geometric Series can be used to represent some functions as power series To use the Geometric Series formula, the function must be able to be put into a specific form, which is often impossible However, use of this formula does quickly illustrate how functions can be represented as a power series)( )( !3 )(''' )( !2 )(" )( !1 )(' )()( 321 Se incluye el término residual para considerar todos los términos desde n1

How Do You Find The Maclaurin Series For F X Ln Cosx Socratic

Taylor Series Tutorial By Chris Tralie

The Taylor series can also be written in closed form, by using sigma notation, as P 1(x) = X1 n=0 f(n)(x 0) n!The result 70 is the same as the result we calculated when we wrote out each term of the Taylor Series individually An advantage of using a for loop is that we can easily increase the number of terms If we increase the number of times the for loop runs, we increase the number of terms in the Taylor Series expansion Let's try 10 terms Note how the line for i in range(10) now includes 10Taylor series expansions of logarithmic functions and the combinations of logarithmic functions and trigonometric, inverse trigonometric, hyperbolic, and inverse hyperbolic functions

Cochranmath Taylor Series Integration And Differentiation

Taylor Series Wikipedia

Free Taylor/Maclaurin Series calculator Find the Taylor/Maclaurin series representation of functions stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyOur next example is the Taylor's series for 1 1 x;La tabella degli sviluppi di TaylorMcLaurin, o tabella degli sviluppi fondamentali, è un elenco che fornisce gli sviluppi in serie di Taylor con centro x 0 =0 per le funzioni elementari e che può essere usato nelle applicazioni teoriche e pratiche, dandoli per assodati Nella precedente lezione abbiamo introdotto gli sviluppi in serie di Taylor, mostrando la definizione e spiegando sotto

Maclaurin Series For Ln 1 X How To Steps Video Lesson Transcript Study Com

Finding Radius And Interval Of Convergence Of A Taylor Series Krista King Math Online Math Tutor

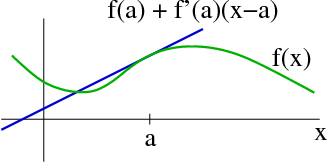
And is f(a)=log(1a) Assuming a > 1 What do you get when you take the derivative of log(1x)?May 11, 17 · Cálculo Avanzado – Carlos L Di Prinzio 5 Figura 1 Distintas aproximaciones a la función f(x) en el punto x=a Entonces la Serie de Taylor queda de la siguiente manera Rnax n af ax af ax af ax af afxf n n )( !Geometric Series Integration of power funct

Series De Taylor

Taylor Series Expansions Of Logarimathic Functions

This is known as the Maclaurin series Example Maclaurin series of 1/(1x) is given by 1xx 2 x 3 x 4 , Applications of Taylor Series The uses of the Taylor series areTaylor Series Calculator with Steps Taylor Series, Laurent Series, Maclaurin Series Enter a, the centre of the Series and f(x), the function See ExamplesApr 15, 18 · 1 Taylor Series By M Bourne Our aim is to find a polynomial that gives us a good approximation to some function (See why we want to do this in the Introduction) We find the desired polynomial approximation using the Taylor Series If we want a good approximation to the function in the region near `x = a`, we need to find the first, second, third (and so on) derivatives

Expand E X Log 1 Y By Maclaurin S Theorem Up To The Third Degree Term Sarthaks Econnect Largest Online Education Community

Approximating Sine X With A Taylor Series In C And Having A Lot Of Problems Stack Overflow

Expansions Which Have LogarithmBased Equivalents Summantion Expansion Equivalent Value Comments x nCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyAnd is f(a)=log(1a) Last edited Sep 17, 11 Sep 18, 11 #6 gb7nash Homework Helper 805 1 uppaladhadium said In taylor series if f(x)=log(1x) then is f'(a)=0?

Taylor Series Maclaurin Series With Examples Calculus How To

Natural Logarithm Series

Answer to 18 (5 pts) The Taylor series approximation for log(1 x), where log is the natural logarithm and 3 2 73 4 log(1 x) =xFree series convergence calculator Check convergence of infinite series stepbystep This website uses cookies to ensure you get the best experience

Maclaurin And Taylor Series Power Series Expansion Of Logarithmic Function

Log Taylor Series Page 1 Line 17qq Com

Maclaurin Series For Ln 1 X How To Steps Video Lesson Transcript Study Com

Taylor Series For Ln 1 X How To Steps Math Class 21 Video Study Com

Taylor Series Expansion With Python Data Science Fabric

Natural Logarithm Wikipedia

Consider The Taylor Series Expansion Ln 1 X Chegg Com

Logarithms Logs Log Ln Lg

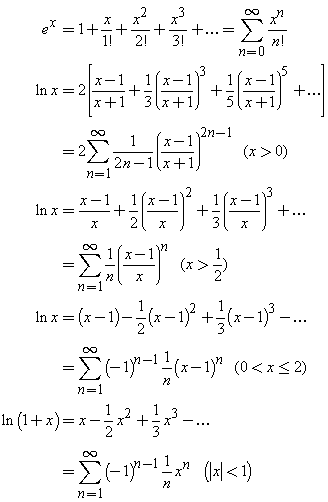
Series Expansions Of Exponential And Logarithmic Functions

Solved Problem 5 Equation 1 Is The Infinite Taylor Serie Chegg Com

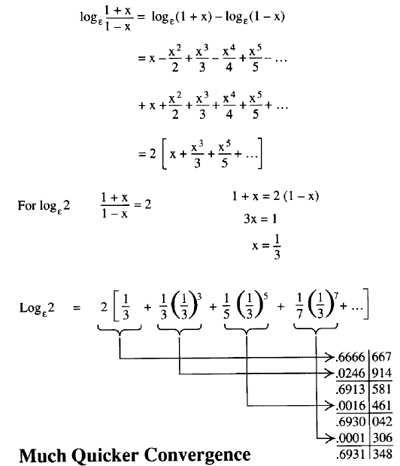
Logarithms Logs Log Ln Lg

Taylor Series For Log X Physics Forums

Log Taylor Series Page 1 Line 17qq Com

Natural Logarithm Wikipedia

Solved Find The Taylor Series For F X 1 X 2 Centered A Chegg Com

Taylor Series Ln 1 X Blog Lif Co Id

Taylor Series Wikipedia

Maclaurin And Taylor Series Introduction A Wide Range

How To Use The Maclaurin S Series To Estimate The Value Of Ln 0 9 To 8dp Quora

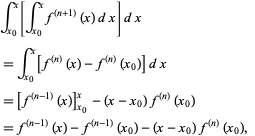
Taylor Series From Wolfram Mathworld

Taylor Maclaurin Polynomials Practice Khan Academy

Approximating Roots Of The Truncated Taylor Series Of Exp By Values Of The Lambert W Function Mathematics Stack Exchange

Worked Example Recognizing Function From Taylor Series Video Khan Academy

Taylor Series Wikipedia

Taylor And Maclaurin Series

Taylor Series Wikipedia

Finding Radius And Interval Of Convergence Of A Taylor Series Krista King Math Online Math Tutor

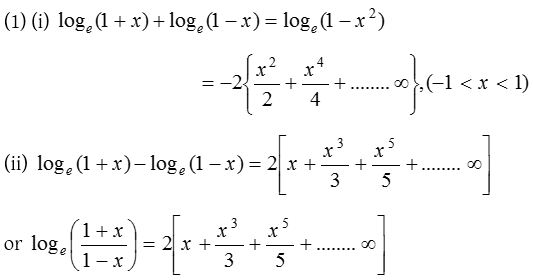
What Is Logarithmic Series Expansion A Plus Topper

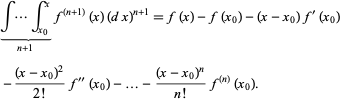
Taylor Series From Wolfram Mathworld

How To Apply Taylor Series Expansion To An Image In Opencv Stack Overflow

Taylor Series In Python Python For Undergraduate Engineers

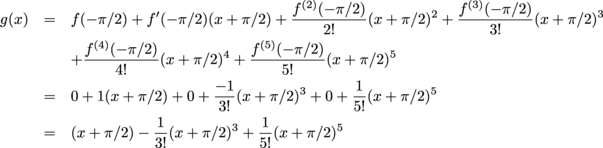
Taylor And Maclaurin Series Exercises

Taylor Series Approximation For 1 Sqrt 1 X 2 Doesn T Quite Add Up Calculus

Taylor Series Ppt Video Online Download

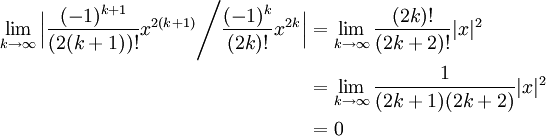
The Maclaurin Expansion Of Cos X The Infinite Series Module

Maclaurin And Taylor Series Power Series Expansion Of Logarithmic Function

Taylor Series Wikipedia

Question Video Finding The First Four Terms Of A Taylor Series Of A Product Of Functions Nagwa

Taylor Series Ln 1 X Blog Lif Co Id

Taylor Series Wikipedia

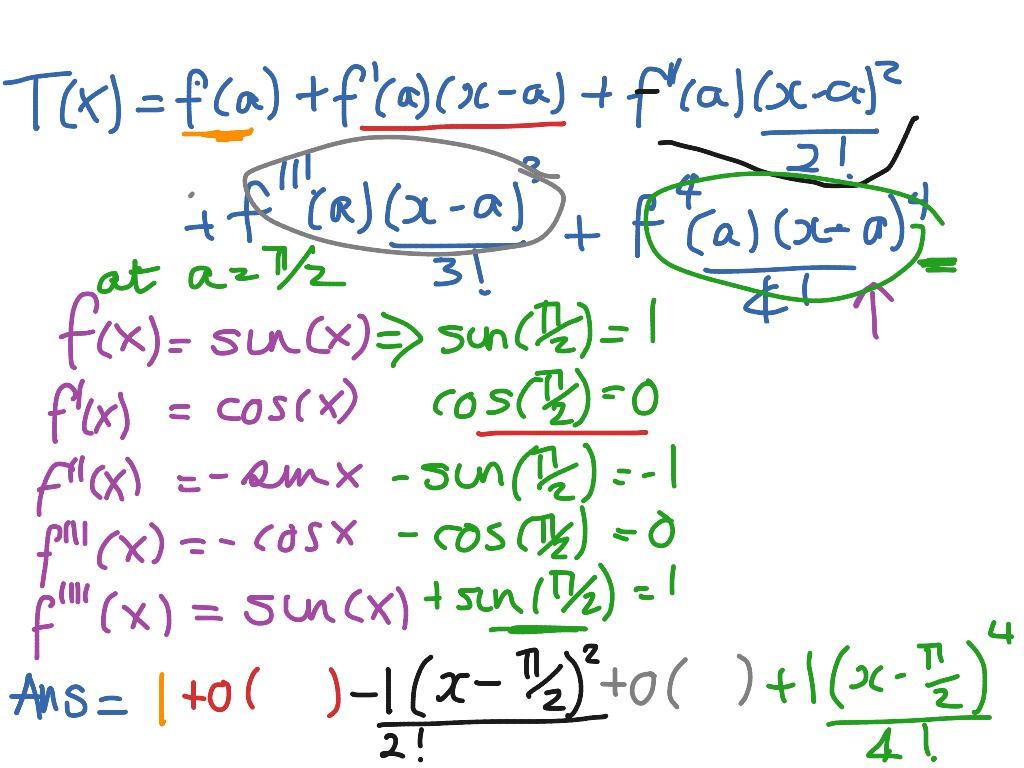
Taylor Series Of Sin X At Pi 2 Math Calculus Taylor Series Showme

Taylor Series Natural Log Page 1 Line 17qq Com

Maclaurin Expansion For 1 Sqrt X 2 9 Mathematics Stack Exchange

Taylor Series For Log X Physics Forums

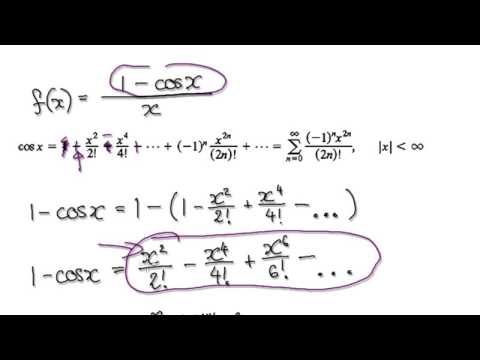
Video 2776 Maclaurin Series 1 Cosx X Practice Youtube

Worked Example Recognizing Function From Taylor Series Video Khan Academy

What Is The Taylor Series Expansion Of Sin X Quora

Series Expansion Calculator Wolfram Alpha

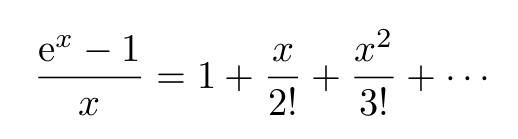
On The Sums Of Series Of Reciprocals By Marco Tavora Ph D Towards Data Science

Taylor Series Tutorial By Chris Tralie

Taylor Series

8 8 Taylor Series Mathematics Libretexts

Taylor Series Expansion Of Natural Log Function Youtube

What Is The Correct Radius Of Convergence For Ln 1 X Mathematics Stack Exchange

The Natural Logarithm And Its Series Expansion 2 Ways Ln X 1 At 0 Youtube

Cochranmath Taylor Series Integration And Differentiation

Tutorial Explicacion Serie De Taylor Mclaurin De Ln X En X 1 Ejercicio Resuelto Youtube

Natural Logarithm Series

What Is The Expansion Of Log 1 X Quora

Finding The Natural Logarithm Of A Number Using Taylor Series In C Stack Overflow

Expand Log 1 Sinx Up To The Term Containing X 4 By Using Maclaurin S Theorem Sarthaks Econnect Largest Online Education Community

Power Series And Polynomial Approximation

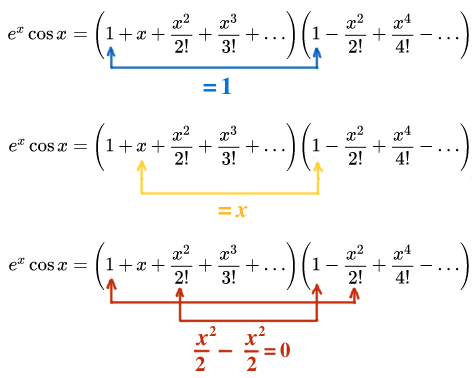
Taylor Series Manipulation Brilliant Math Science Wiki

How Do You Do The Taylor Expansion For F X Log X 1 At X 0 Socratic

Taylor Series For F X Ln X Centered At X 1 Youtube

Serie De Taylor Maclaurin Del Logaritmo Natural Youtube

Taylor Series Wikipedia

Incoming Term: serie taylor log(1+x), serie di taylor log(1+x),